One of the most widely used types of unsupervised ML is $k$-means clustering. With this technique, $k$ represents a given number of clusters (decided by the user) and observations are categorized such that those that fall into the same cluster are the most like each other, while simultaneously being as dissimilar as possible to the observations in other clusters.²² 2 Goodfellow et al (2016) define unsupervised learning as any technique that determines information from a “distribution that (does) not require human labor to annotate examples”.

Note that, by applying unsupervised learning to our return pairs, we do not make any claims as to what type of returns they are. We simply run them through an unsupervised learning algorithm, which then tells us the type based on the return pairs’ similarities.

As mentioned above, in order to hone in on the low-rate environment, we only consider returns for which the government bond yield for that period is below a certain threshold.³³ 3 We also conducted this analysis for the entire period (ie, without the threshold) and it showed very similar results to those presented. Our yield threshold for the US is 2.5% (ie, for any given month, the US 10-year Treasury yield at the beginning of that month must be below 2.5% in order for the return pair for that month to feature in our analysis). This threshold was chosen to ensure that the analysis applies to a low-rate environment while including a reasonably large number of return pairs. In Figure 1 we show the results of the $k$-means clustering algorithm run on these US returns when $k$ is equal to 2 or 3.⁴⁴ 4 The algorithm is not actually applied on the returns themselves but on their standardized $z$-scores. We then map the clustered $z$-scores back onto their return equivalents.

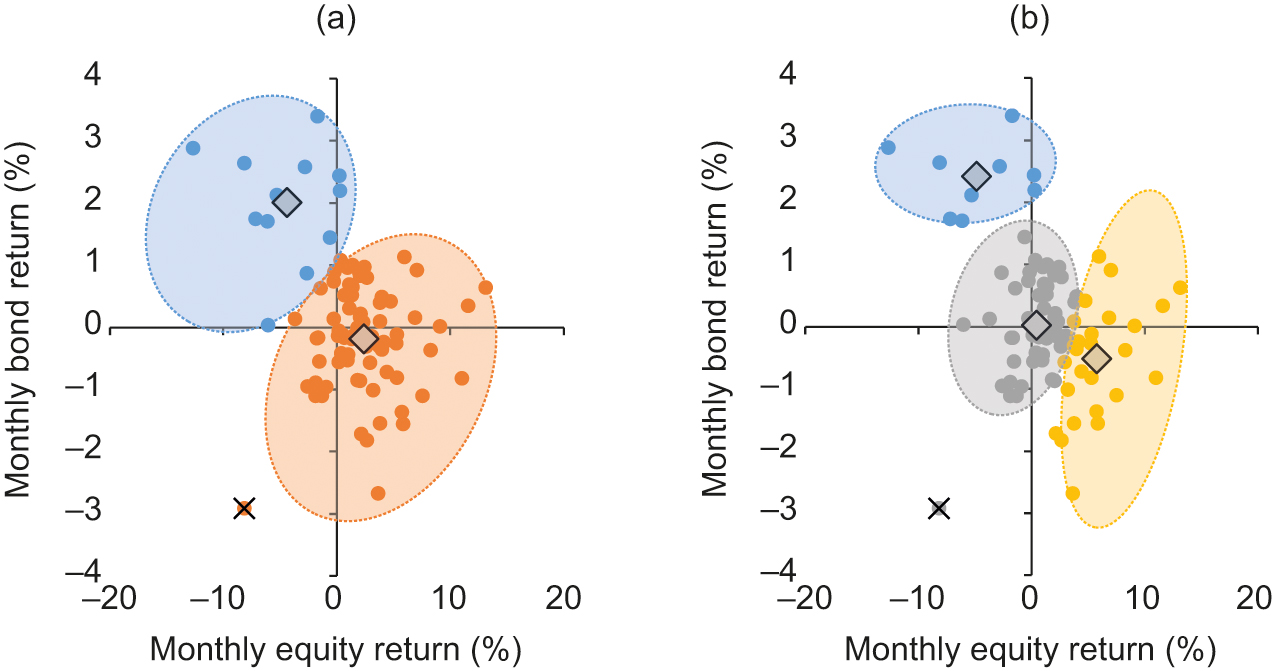
Each of the clusters is given a color. We observe that for $k=2$, some returns are categorized as orange (in which equities have almost always had positive performance and bonds are slightly negatively tilted) and some as blue (in which bonds have almost always shown positive performance and equities have shown negative performance). In other words, this suggests a negative relationship between US equity and US Treasury returns and that when equities go up, the bond return is not easily predictable but, when equities go down, bonds almost always go up. Importantly, we do not see a cluster located in the “down–down” quadrant, implying that the few pairs of returns that do fall in this region are anomalous and not statistically relevant. For $k=3$, the situation is very similar. The blue “down–up” state largely remains unchanged, while the orange “up–down” state splits into two distinct market states: gray and yellow. This reinforces the hypothesis that bonds provide good diversification for equities, as again we do not see a cluster toward the bottom-left corner mapping a “down–down” market state.

The diamonds depict each cluster’s centroid, which is not an actual return pair but rather the notional center of each cluster. For the example of $k=2$, this categorization can be thought of as two market state centers: one that has equities up and bonds slightly down and one that has equities down and bonds up. For $k=3$, we still have our state in which equities are down and bonds are up, and our “equities up” state now divides into two further states: one where bond returns are more centered on 0% and one where they are negative. This further confirms the idea that US Treasuries act as a counterbalance to equity movements.

To further corroborate the fact that the return pairs in the “down–down” quadrant are anomalous and not statistically relevant, we performed an anomaly detection analysis. Some papers (see, for example, Barai and Dey 2017) have used clustering techniques to perform anomaly detection, which helps to distinguish which observations may not be meaningful based on how far away they lie from their corresponding cluster centroid. We performed a version of this (see Appendix 1 online) to assess which observations may be anomalies, denoted in the figures by black crosses. We observe that, irrespective of whether $k=2$ or $k=3$, there is a single anomaly that lies in the bottom-left quadrant. Intuitively, this suggests that scenarios in which equities and bonds have negative unidirectional returns are rare and can be considered anomalous, further corroborating the conclusion that bonds act as a good hedge for equities.

We also mentioned earlier that an alternative approach to this analysis might be to run a linear regression in order to gain a sense of the bonds’ average response for a given change in equities. However, a line of best fit through these data points would be unable to explain a large percentage of the variance (ie, it would have a low $R$-squared value, in this case equal to 9.9%) due to the large dispersion of the return pairs. Therefore, while it might provide some indication as to the typical directionality of the relationship, it would not help much in understanding the different market states that our clustering analysis gives us. More detail on such an approach is provided in Appendix 2 (online).

At this stage, there are two questions: “Should we use $k=2$ or $3$?” and “Why should $k=2$ or $3$?” We used two well-established techniques to determine the appropriate number of clusters (see Appendix 3 online). Our results suggest that the use of two clusters is the best choice for the US data based on both validation methods.⁵⁵ 5 Some qualitative judgment is still required when choosing an appropriate value for the number of clusters – in this, parsimony is often best. In fact, it can be the case that some of the validation methods (eg, silhouette score) suggest multiple clusters to be optimal, which can lead to overfitting.

This result is important because it suggests that there are most likely no more than two main states that are consistent with the underlying pattern of equity and bond returns and that these two states (“up–down” and “down–up”) identified by the clusters correspond to US equities and government bonds balancing one another. Other return pairs are interpreted as not statistically significant deviations from these two main states. The fact that, when we increase the number of clusters to three, the “up–down” cluster is further split into two new clusters and the three centroids are aligned on an imaginary negatively sloped line confirms the diversification properties of government bonds.

A key advantage of this analysis over a regression-based approach is the identification of market states. In addition to providing information on the (linear) relationship between equities and bonds, $k$-means clustering enables us to identify any clustering that may be consistent with the presence of a specific market state (eg, “down–up”). The combination of using the optimal number of clusters and their locations helps to assess whether there is sufficient evidence for such a state to exist. Moreover, with $k$-means clustering, the absence of clusters can also provide valuable insight into whether observations located in these regions are likely to recur in the future.

Of course, not all multi-asset investors choose to invest exclusively in US funds. For this reason, we also examine global returns to see whether this relationship holds for global investors. Figure 2 shows the same $k$-means analysis when using $k$ equal to 2 or 4 for global returns. Here, we set our yield threshold equal to 1.5% using a global Treasury index that resulted in a similar number of return pairs as the US example.

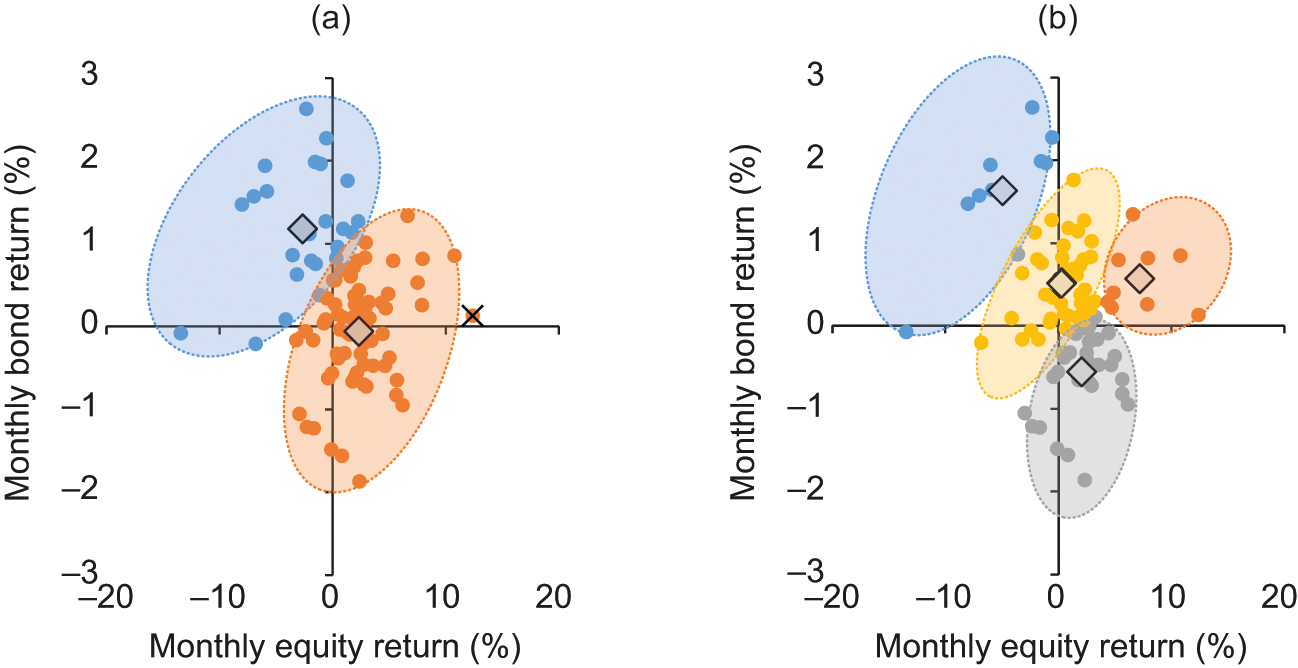
We see similar results as those in Figure 1, in the sense that two clusters show a clear diversification benefit with similar locations for the two centroids and, as a regression analysis would suggest, express a negative relationship between global equity returns and government bond returns. Again, there is no mapping to the “down–down” state, although one key difference from the US analysis is that an anomaly is detected in the top-right quadrant when $k=2$, again suggesting that such unidirectional returns are rare. Therefore, at least in the paradigm of two clusters being appropriate, there seems to be little difference between US and global returns, with both characterizing recurrent market states as “equities up/bonds down” and “equities down/bonds up”.

Another difference between the global analysis and the US one is demonstrated in Figure A-4 (see the online appendix). Although it suggests that setting $k=2$ is still best when both the maximum silhouette score and the elbow occur at this point, in this case we see that $k=3$ has a lower silhouette score than $k=4$, which is why we present our clustering with $k=4$. However, there is still no cluster or centroid that lies in the bottom-left quadrant. Also, for $k=4$, no anomalies were detected.