Does the impact of exchange-traded funds flows on commodities prices involve stockpiling as a signature? An empirical investigation

Steve Ohana; Xiaoying Huang

1 Introduction

The financialization of commodity markets has triggered a heated debate among professionals, researchers and policy makers.

In the literature on “the impact of speculation” on commodity futures markets, commodity index investing, a financial innovation that emerged as a standard investment practice among portfolio managers in the mid-2000s, has attracted particular attention. Index funds track indexes composed of baskets of commodity futures that are regularly rolled over prior to their expiration. While causality tests generally refute the hypothesis that index flows Granger-cause commodities’ prices, some more recent studies have uncovered a contemporaneous impact of weekly index flows on some energy futures prices.¹¹Precise references are provided in the next section.

Two opinions exist at the theoretical level about the origin of an abnormal speculative impact on commodities’ prices. Paul Krugman (2008a,b) and other authors consider that speculation in commodities’ paper markets can only have an impact on commodity prices through a change in inventory or in the commodities’ forward term structure. From this perspective, absent abnormal stockpiling or a change in the term structure, speculation should not be blamed for abnormal price distortions in commodity markets. By contrast, Pierru and Babusiaux (2010) argue that, due to the short-term price inelasticity of supply and demand in commodity markets, an abnormal speculative impact on commodities prices can occur without involving stockpiling as a signature. More details regarding these two positions will be provided in the next section.

This paper examines the relation between the flows into the three main commodity index exchange-traded funds (ETFs) and the prices, inventory and term structure of four energy and twelve US-traded agricultural contracts. Although a positive relation is found between price and index flows for a large proportion of energy and agricultural markets, the impact occurs without any change in inventories or in the futures prices term structure. In addition, the relation of index flows to commodity prices disappears beyond a certain time horizon, suggesting a short-lived market impact followed by a correction. Overall, our results suggest that abnormal speculation can distort commodities prices without involving stockpiling as a signature.

The rest of this paper is organized as follows. Section 2 reviews the previous literature; Section 3 presents our measures for term structure and index flows; Section 4 presents our empirical strategy and discusses the results; Section 5 extends our framework to agricultural contracts; and Section 6 concludes.

2 Theoretical background

As part of the discussion surrounding the relation between commodity price and speculation, Paul Krugman (2008a) mentioned in a New York Times blog post that “the only way speculation can have a persistent effect on oil prices, then, is if it leads to physical hoarding – an increase in private inventories of black gunk”. In another blog post (Krugman 2008b), he argued that the impact is possible only if “someone who actually has oil” sells oil to a long speculator through a forward contract and “holds oil off the market so he can honor that contract when it comes due”. Let us remark that not only storers but also producers may have the ability to “hold a commodity off the spot market” with a view to honoring a short position in the paper market. Because storers and producers must be incentivized to hold the commodity off the spot market, such a mechanism should be revealed by a change in the inventory or at least in the forward term structure (if producers are involved rather than storers). Hence, from this perspective, speculation cannot drive prices away from the fundamentals without a change in inventories (or in the futures prices term structure). This argument is illustrated in Figure 1.

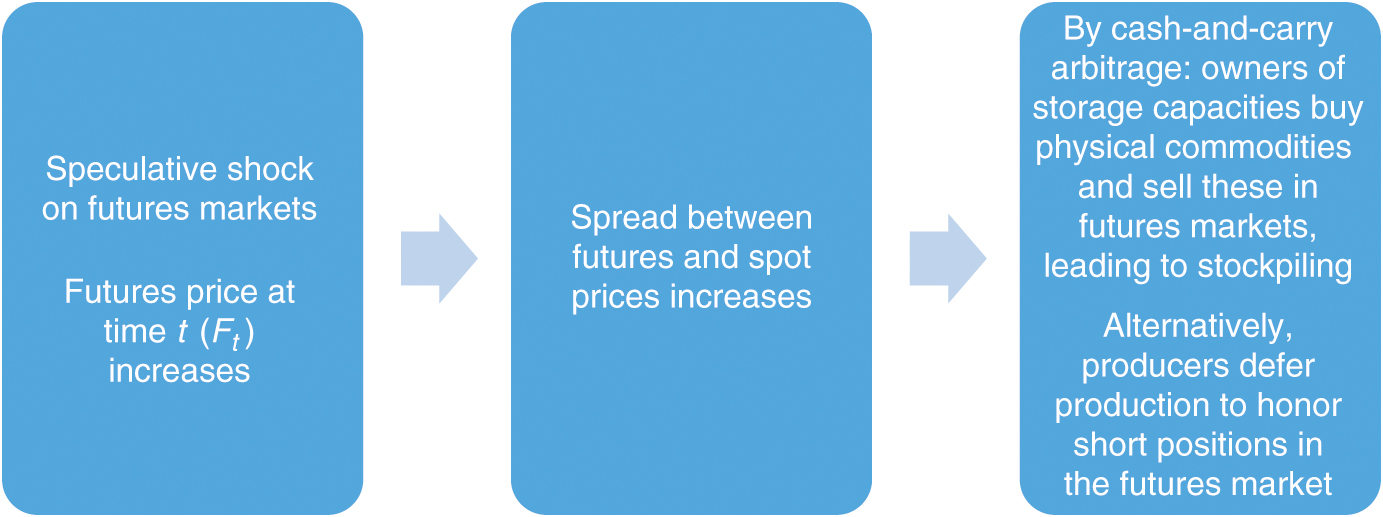
Figure 1: Price–term structure–inventory–flows relation in Hypothesis 1.

Figure 1: Price–term structure–inventory–flows relation in Hypothesis 1.

An alternative story, albeit along the same lines, proceeds as follows: should unwarranted speculative activity drive prices away from the “fundamental” price (which may be defined as the price that balances production with consumption in the medium term), then, if the price and demand functions are sufficiently price elastic, an excess of production should ensue, resulting in inventory accumulation. Hence, also in this case, an abnormal speculative impact should be associated with a change in inventory. However, inventory accumulation would then be the consequence of the abnormal price rise, not its cause (see Pirrong 2008).

An opposite view, proposed by Pierru and Babusiaux (2010), holds that speculation can have an impact on commodity prices without stockpiling as a signature. The argument relies on the low short-term price elasticity of supply and demand in commodity markets, leading to minimal demand and supply reactions, and, hence, minimal inventory adjustments in the case of an exogenous price rise. In their view, demand is inelastic in the short run and adjusts gradually. Inventory shock $\Delta I$ after an increase of prices due to a speculative shock can be defined as a function of demand elasticity $\xi(t)$ and price changes $\Delta S$ , with $\Delta I=\xi(t)\Delta S$ . $\xi(t)$ is supposed to be an increasing function of time $t$ : $\xi^{\prime}(t)>0$ . Following a speculative shock on the prices, and given short-run price inelasticity, if prices promptly revert to normality, stockpiling will not be observed. The underlying economic mechanism may be illustrated as in Figure 2.

Figure 2: Price–term structure–inventory–flows relation in Hypothesis 2.

Figure 2: Price–term structure–inventory–flows relation in Hypothesis 2.

The question of the price impact of uninformed speculative flows on commodity prices has received much attention in the recent literature. The debate originated with the hypothesis of Masters (2008) that index investment flows had been a major contributor to the energy prices rise of 2007–8. A large number of studies have tried to identify the direction of the causality between prices and flows by performing a Granger causality test between investment flows and prices, or, alternatively, by analyzing the relationship between flows and subsequent price returns at the cross-sectional level (see, for example, Irwin and Sanders 2010, 2011; Sanders and Irwin 2017; Büyüksahin and Harris 2011; Capelle-Blancard and Coulibaly 2011). Most studies in this strand of the literature reach the conclusion that flows do not “Granger cause” price changes. However, temporal precedence is not equivalent to causation, and the usefulness of the Granger causality test is limited (Grosche 2014). Singleton (2013) observes that the thirteen-week rolling cumulative index flows predict the subsequent oil prices’ weekly returns after controlling for fundamental financial and nonfinancial variables (convenience yield, equities prices returns, financing conditions offered by large investment banks, etc). The documented instability of the precedence relation between flows and prices is an additional concern. For example, Robles et al (2009), who carry out Granger causality tests on sliding thirty-month windows, show that the hypothesis that flows “Granger cause” prices is sometimes rejected and sometimes validated, depending on the period of the test.

Gilbert and Pfuderer (2014) find a significant positive association between contemporaneous weekly index flows and price variations for agricultural commodities. Hendersen et al (2012) use commodity linked note (CLN) issues as a plausibly exogenous index flows variable. Through an event-study analysis, they observe the existence of an impact of CLN issues on commodities prices. Guilleminot et al (2014) also address the question of endogeneity by using index flows into twelve agricultural contracts and three generalist ETF as two possibly exogenous index flows variables. They find an economically and statistically strong association of weekly index flows to futures price returns in some agricultural markets, the effect being reinforced in conditions of overall financial stress.

Although the literature tends to conclude that index flows do have a contemporaneous effect on commodity price returns, the relationship between commodity index funds, on the one hand, and inventory changes or the term structure of futures contracts, on the other hand, has so far received little attention. Mou (2011) shows that a strategy front-running Goldman Sachs Commodity Index (GSCI) investors just a few days before the monthly rolling of the positions yields abnormal returns. The abnormal return disappears if the strategy is executed on contracts, which are not included in the GSCI. This suggests that GSCI investors cause the spread between first-nearby and second-nearby contracts to widen (the first-nearby contract, which is sold by the GSCI investor, depreciates with respect to the second-nearby, which is bought by GSCI investors) at the time of the rolling. Using available oil inventory data, Lombardi and Robays (2011) find no significant impact of “destabilizing speculation” on inventories.

Our aim in this paper is to test the two aforementioned hypotheses regarding the impact of uninformed index speculation on commodity prices. Hypothesis 1 states that this impact involves a change in the term structure and/or inventories as a signature; by contrast, Hypothesis 2 assumes that this impact goes directly through the prices without involving any change in inventories or the term structure. Overall, our results give strong support to the second hypothesis. An additional implication of our observations is that the market impact of ETF flows vanishes beyond a certain time horizon, depending on the commodity market considered.

3 Term structure and index funds

3.1 Term structure and its determinants

Investigating the impact of index funds on energy commodities’ futures calendar spreads requires controlling for various variables that are likely to drive commodities prices’ term structure.

The possibilities of arbitrage between spot and futures markets for storable commodities strongly attach the spread between spot and futures prices to the total charge of carrying forward a commodity from the present date to the futures contract maturity. This charge, in turn, is composed of the capital charge (ie, interest rates), storage costs and the “price of storage” (see Working 1949), ie, the price of renting a free storage space from the present date to the contract maturity. This price of storage naturally increases with the level of inventories, as high inventories imply scarce residual storing capacities.

When inventories are depleted, the price of storage turns negative as free storage space is abundant and diverse financial benefits (often referred to as the “convenience yield”) accrue to the holder of a physical commodity.

“Backwardation” corresponds to a situation in which the futures term structure curve (the behavior of futures prices as a function of contract maturity) is downward sloping. According to the theory of storage, backwardation occurs when the convenience yield is greater than the cost of holding inventory (interest rate and cost of storage); hence, when inventory is low. The opposite situation (when the futures price is higher than the spot price) is referred to as “contango”.

Backwardation determines, in turn, the storage behavior. Telser (1958) points out that investors tend to store in a situation of contango and sell inventory in a context of backwardation. Moreover, since long-dated futures contracts are less expensive, rolling from nearer to longer contracts is beneficial for speculators in backwardated markets. Hence, the term structure influences not only storers’ but also financial speculators’ behavior in commodity futures markets.

The relation between inventory and futures term structure is now well established. Working (1933) was the first to identify the strong positive correlation between futures calendar spreads (the difference between long- and short-dated maturities) and inventory level in the wheat market. This relation between inventory and futures calendar spreads has been retrieved for different commodity markets and in more recent periods (see, for example, Fama and French 1988; Gorton et al 2007; Geman and Ohana 2009). The relation goes both ways. An inventory increase raises the price of storage (ie, the price to rent a free storage space), which can be readily expressed in terms of the spread between the futures prices of long- and short-dated maturities. Conversely, an increase in the spread between long- and short-dated futures prices prompts market participants to execute the cash-and-carry arbitrage, resulting in an increase of inventories.

However, short-dated contracts can be highly volatile (see Borovkova 2003); hence, the spread between the two nearest contracts might contain “noise”. Another concern is seasonality: the term structure behavior is affected by the timing of the production or consumption, and the spread between different contracts is strongly discontinuous at the crossing of rolling dates (ie, jumps after the nearest contract ceases trading). In order to circumvent these problems, we use the smooth term structure indicator introduced in Guilleminot et al (2014), defined as the performance of a strategy shorting the first-nearby (denoted by F1), while buying the contract delivering one year after the first-nearby (F2):

\operatorname{TS}(t)=\prod_{i\leqslant t-\Delta t}\bigg(1+\frac{\mathrm{F}2_{i% +\Delta t}-\mathrm{F}2_{i}}{\mathrm{F}2_{i}}-\frac{\mathrm{F}1_{i+\Delta t}-% \mathrm{F}1_{i}}{\mathrm{F}1_{i}}\bigg).

(3.1)

$\Delta\mathrm{TS}_{[{t_{1};t_{2}}]}=\operatorname{TS}(t_{2})-\operatorname{TS}% (t_{1})$ reflects the change in the term structure and in inventory anticipations by market participants between dates $\smash{t_{1}}$ and $\smash{t_{2}}$ .

Three variables are included as control variables in the regressions of futures prices and term structure changes on index flows: interest rate, dollar index and hedging pressure.

3.1.1 Interest rates

Since interest rates determine the cost of carrying forward a commodity, a positive correlation between interest rate changes and changes in term structure is expected. In addition, due to the positive correlation of commodity prices to inflation surprises and the reaction function of the Federal Reserve’s target rates to inflation, we may expect a positive correlation of interest rate to commodities prices. The six-months US Treasury bill yield is chosen in our case.

3.1.2 Dollar index

Most commodities are quoted in US dollars. A dollar depreciation induces an upward pressure on the dollar-labeled price since, all else being equal, commodities become cheaper for investors outside the United States. In this paper, we use the so-called dollar index as a proxy for the value of the US dollar. This is defined as the value of the US dollar against a trade-weighted basket of other currencies. While a negative relation is expected between dollar index and commodities’ price in dollars, it is harder to conjecture on the correlation of dollar index to inventory/term structure shocks.

3.1.3 Hedging pressure

Hedging pressure is considered as a measure of risk premium, which can be referred to as the net demand for long positions from hedgers in futures markets. Keynes (1930) points out that risk aversion of inventory holders and producers induces “normal backwardation”, ie, futures prices below the expected spot prices at maturity. The traditional measure of hedging pressure is as follows:

\mathrm{hedging~{}pressure}=\frac{\mathrm{long~{}hedging~{}positions}-\mathrm{% short~{}hedging~{}positions}}{\mathrm{long~{}hedging~{}positions}+\mathrm{% short~{}hedging~{}positions}}.

(3.2)

In this paper, long (short) hedging positions are the long (short) aggregate commercial positions as outlined in the Commodity Futures Trading Commission (CFTC) weekly report on US derivatives markets. Depending on whether hedging trading activity is focused on long- or short-term futures contracts, hedging pressure may increase or decrease the contango of the curve. Regarding the link of hedging pressure to the futures price itself, it could be argued along with Keynes that an increase in the hedging pressure, reflecting an additional need of long positions from hedgers, may exert an upward pressure on the prices. Alternatively, a negative relation between prices and hedging pressure may arise from the endogeneity of commercial positions to the prices, since we know from Moskowitz et al (2012) that speculators benefit from momentum at the expense of hedgers in futures markets.

It is therefore a matter of empirical investigation as to whether the relation between hedging pressure and the term structure/futures prices is positive or negative.

3.2 Commodity ETF flows

In the rest of this paper, we define “index flows” as the flows into the three main ETFs tracking general commodity indexes: the GSCI, the Bloomberg Commodity Index, (formerly called the Dow-Jones UBS Commodity Index) and the Deutsche Bank Commodity Index.²²The three global commodity index ETFs considered are Powershares DB, the IPATH Bloomberg Commodity Index and ISHARES S&P GSCI. They represent the lion’s share of ETF investment into generalist commodity indexes.

The four energy futures that are the object of our first study are the crude oil, heating oil, RBOB gasoline and natural gas NYMEX contracts, which are included in these major commodity indexes. Specifically, energy commodities have a combined weight of almost 80% in the GSCI and about 30% in the Bloomberg Commodity Index, with only crude oil and heating oil being included in the Deutsche Bank Commodity Index. Therefore, we are aware of a potential endogeneity problem when assessing the impact of ETF flows on energy prices, as ETF investors may be partially driven by the oil prices. To alleviate this concern, we conduct in Section 5 additional tests on twelve US-traded agricultural contracts, for which ETF flows appear more exogenous. Indeed, agricultural commodities weigh 10% and 30%, respectively, in the GSCI and Bloomberg Commodity indexes, and the correlation of grains prices to a global commodity index computed as the equal-weighted average of the GSCI and the Bloomberg Commodity Index has been around 50% since 2006. The correlation falls to less than 40% for meat and other soft products. This pales in comparison to the over 90% correlation observed between the West Texas Intermediate (WTI) crude price and the average commodity index. Therefore, index flows toward broad commodity indexes such as the GSCI or the Bloomberg Commodity Index could follow the trend set in the energy markets but probably not specific agricultural price dynamics.

Our measure of index flows has several advantages over the “commodity index traders’ positions” from the CFTC reports. First, for energy contracts, the CFTC reports fail to properly disentangle index positions from commercial positions. Second, even for agricultural contracts, a part of the index positions consists of investments into general agricultural commodity indexes (consisting of baskets of agricultural contracts only) and into single commodity indexes. As a result, the “CIT positions” from the CFTC reports are more endogenous in nature than the ETF flows, which only include investments into the broad commodity indexes.

ETF flows on the three indexes between the weeks $t-1$ and $t$ are defined as follows:

\mathrm{flows}_{t,t-1}=\sum_{i=1}^{3}\mathrm{ETF~{}price}_{t}^{i}(\mathrm{% shares}_{t}^{i}-\mathrm{shares}_{t-1}^{i}),

(3.3)

where $\smash{\mathrm{ETF~{}price}_{t}^{i}}$ denotes the price of ETF share of index $i$ at week $t$ and $\smash{\mathrm{shares}_{t}^{i}}$ refers to the total number of ETF shares issued for the $i$ th ( $i=1,2,3$ ) ETF at week $t$ .

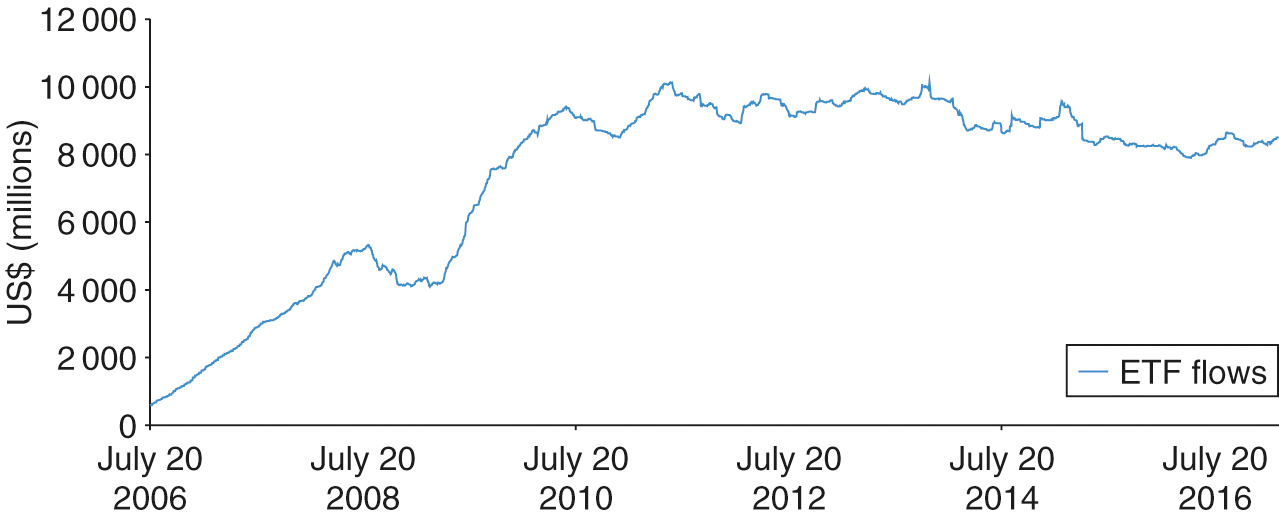
Figure 3: Cumulative investment flows into the three main commodity ETFs. The graph shows the cumulative weekly inflows into the three ETFs, tracking the major commodity indexes from July 2006 to December 2016.

Figure 3: Cumulative investment flows into the three main commodity ETFs. The graph shows the cumulative weekly inflows into the three ETFs, tracking the major commodity indexes from July 2006 to December 2016.

Figure 3 shows the cumulative investment flows into the three major ETFs from July 2006 to December 2016. After a first wave of investment into commodities’ indexes up to July 2008, where around USD5 billion was poured into commodity ETFs, a divestment of around USD1 billion ensued on the occasion of the 2008 financial crisis. After March 2009, a new wave of investment of around USD6 billion launched up to May 2011, after which index investors withdrew USD2 billion from commodity ETFs at a slow but steady pace until December 2016.

4 Empirical analysis

4.1 Primary analysis using weekly EIA inventory data

In a first analysis, we use real inventory data from weekly US Energy Information Administration (EIA) reports from July 2006 to December 2016. As crude oil is used as an input for the production of petroleum products, the crude oil regression is based on the weekly US ending stocks of crude oil and petroleum products. For the three other products, we use the corresponding US ending stock from the EIA report, released every Friday. We filter out the strong seasonal component in natural gas inventory data by calculating the deviation of the inventory in a given week to the average inventory the same week over the last five years.

The regression is conducted as follows (the index $i=1,2,\dots,4$ corresponds to the energy contract considered):

\Delta\mathrm{inventory}_{i,t}=a+\beta\,\mathrm{ETF~{}flow}_{i,t}+\varepsilon_% {t}.

(4.1)

According to Table 1, direct regressions of weekly inventory changes on index flows do not lend support to the hypothesis of an impact of index flows on inventories.

Table 1: Regression of inventory changes on ETF flows for crude oil, gasoline, heating oil and natural gas in the United States. [Here we report the regression coefficients and

R

-squared of the following OLS regressions:

\Delta\text{inventory}_{i,t}=\alpha+\beta\Delta\text{ETF~{}flows}_{i,t}+% \varepsilon_{i,t}

.

\Delta\text{inventory}_{i,t}

is the weekly US inventory change, computed from the EIA report (released each Friday). We use the crude oil and refined petroleum products inventory in the crude oil regression. “ETF flows” refers to the weekly investment flows into the three main ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 524 (weekly data from July 2006 to December 2016).]

Inventory	ETF	$R^{\textbf{2}}$
Crude oil	$-$ 0.01 (0.89)	0.001
Gasoline	$-$ 0.02 (0.51)	0.001
Heating oil	$-$ 0.05 (0.25)	0.002
Natural gas	0.03 (0.48)	0.001

4.2 Term structure and index funds flows

To estimate the impact of index flows on the term structure, we perform a simple linear regression of term structure changes on ETF flows, while including the aforementioned control variables:

\Delta\mathrm{term~{}structure}_{i,t}=\alpha+\beta\,\mathrm{ETF~{}flows}_{i,t}% +\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}.

(4.2)

The term structure of an energy product $i$ is defined through (3.1). In Table 2, we observe, as expected, a strong positive relation between inventories and term structure weekly variations for the four energy products. The index $j$ refers to the control variables:

x_{j,t}=(\Delta\mathrm{interest~{}rate},\Delta\mathrm{dollar~{}index},\Delta% \mathrm{hedging~{}pressure}).

Weekly observations are used, ranging from July 2006 to December 2016.

Table 2: Regression of inventory changes on term structure for crude oil, gasoline, heating oil and natural gas in the United States. [Here we report the regression coefficients and

R

-squared of the following OLS regression:

\Delta\text{inventory}_{i,t}=\alpha+\beta\Delta\text{term~{}structure}_{i,t}+% \varepsilon_{i,t}

.

\Delta\text{inventory}_{i,t}

is the weekly US inventory change of commodity

i

, computed from the EIA report (released each Friday). We use the crude oil and refined petroleum products inventory in the crude oil regression. Natural gas inventories are calculated as deviations from the average inventory across the previous five years for the same week of the year.

\Delta\text{term~{}structure}_{i,t}

refers to the change in term structure of commodity

i

in week

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby (NYMEX) futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of each contract.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 524 (weekly data from July 2006 to December 2016).]

changes	coefficients	$R^{\textbf{2}}$
	Term structure
Inventory	regression
Crude oil	0.12 (0.004***)	0.01
Gasoline	0.11 (0.009***)	0.01
Heating oil	0.12 (0.005***)	0.01
Natural gas	0.14 (0.002***)	0.02

In unreported tests, we have tried to include lags both in index flows, prices returns, term structure and inventories. Serial correlation is indeed present in the data, but contemporaneous relations are much stronger than lagged effects and the inclusion of lags did not change the conclusions of this paper.

The results of regression (4.2) are reported in Table 3. Dollar variations do not have a significant impact on the term structure, except for gasoline, where they enter with a positive sign, only significant at the 10% level. Hedging pressure enters with the expected positive sign in the case of heating oil. Finally, interest rate variations enter with an unexpected negative sign in the case of gasoline.

Overall, the results displayed in Table 3 again lend little support to the hypothesis that index funds modify commodities’ term structures or inventories.

Table 3: Regression of term structure on ETF flows for four energy commodities (NYMEX contracts). [Here we report the result of the following OLS regressions for crude oil, heating oil, gasoline and natural gas NYMEX contracts:

\Delta\text{term~{}structure}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\sum_% {j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

.

\Delta\text{term~{}structure}_{i,t}

refers to the change in term structure of commodity

i

in week

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of each contract.

\text{ETF~{}flows}_{t}

denotes the net weekly inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

. The control variables are

x_{j,t}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

.

\Delta r

is the change in the six-month government bill rate.

\Delta\text{dollar}

represents the dollar index return.

\Delta\text{HP}

refers to the change in hedging pressure, which is calculated from the weekly variation of the ratio

(\text{long hedging positions}-\text{short hedging positions})/(\text{long hedging positions}+% \text{short hedging positions})

, computed from the weekly CFTC report (released each Friday but reporting positions from the previous Tuesday). The changes in the variables entering the regression are between consecutive Tuesdays.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 539 (weekly data from July 2006 to December 2016).]

		flows	$\Delta$ HP	$\Delta$ dollar	$\Delta r$	$R^{\textbf{2}}$
		ETF
Crude oil	Estimate	$-$ 0.08	0.04	0.03	$-$ 0.02	0.01
	$p$ -value	0.05**	0.39	0.51	0.57
Gasoline	Estimate	0.01	$-$ 0.01	0.12	$-$ 0.16	0.03
	$p$ -value	0.89	0.87	0.007***	0.0001***
Heating oil	Estimate	$-$ 0.05	0.33	0.10	$-$ 0.06	0.13
	$p$ -value	0.19	$\textbf{6.9e}{-}\textbf{15}$ ***	0.02**	0.17
Natural gas	Estimate	$-$ 0.06	0.05	$-$ 0.02	$-$ 0.003	0.01
	$p$ -value	0.17	0.24	0.62	0.94

4.3 Index funds and futures prices

We now turn to the relationship between index funds and futures prices returns. Some recent studies have uncovered a significant contemporaneous relationship between commodity index positions and energy futures prices.

We double-check this insight by using a regression framework that is very similar to the one above; however, in this instance we use futures prices returns as the dependent variable:

\mathrm{futures~{}returns}_{i,t}=\alpha+\beta\,\mathrm{ETF~{}flows}_{t}+\delta% \Delta\mathrm{term~{}structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i% ,t}.

(4.3)

Futures prices returns are computed from the rolled futures prices series, defined as³³The rolled futures prices series is actually the performance of a strategy longing the first-nearby contract (with the notional position being kept constant at USD1 and rolling over this long position whenever the first-nearby ceases trading).

P_{t}=\prod_{i\leqslant t-\Delta t}\bigg(1+\frac{\mathrm{F}1_{i+\Delta t}-% \mathrm{F}1_{i}}{\mathrm{F}1_{i}}\bigg),

where F1 refers to the prices of the first-nearby contract and $\Delta t$ denotes a period of one trading day. The “rolled futures return” between two different dates $t_{1}$ and $t_{2}$ is in turn computed by

r_{[t_{1};t_{2}]}=\frac{P_{t_{2}}-P_{t_{1}}}{P_{t_{1}}}.

In what follows, we use daily, weekly, bimonthly, monthly, two-month, three-month and four-month time steps for the rolled futures returns calculation.

The control variables are the same as before, except that we now include the term structure as a supplementary control variable.

The results are shown in Table 4. Dollar index returns have a significant negative relation to the futures prices returns in the case of crude oil and heating oil, which is in line with our expectations. The interest rates are positively related to the prices, as was also expected (see Section 3.1).

Table 4: OLS regressions of first-nearby futures prices on ETF flows for four energy commodities (NYMEX contracts). [Here we report the results of the following OLS regressions for crude oil, heating oil, gasoline and natural gas NYMEX contracts:

\text{futures~{}return}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\delta% \Delta\text{term~{}structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

.

\text{futures~{}return}_{t}

represents the return of the rolled futures prices series of commodity

i

in week

t

(strategy longing and rolling over the first-nearby futures contract at the last trading date).

\Delta\text{term~{}structure}_{i,t}

refers to the change in term structure of commodity

i

in week

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of each contract.

\text{ETF~{}flows}_{t}

denotes the net weekly inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

. The control variables are

x_{j,t}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

.

\Delta r

is the change in the six-month government bill rate.

\Delta\text{dollar}

represents the dollar index return.

\Delta\text{HP}

refers to the change in hedging pressure, which is calculated from the weekly variation of the ratio

(\text{long hedging positions}-\text{short hedging positions})/(\text{long hedging positions}+% \text{short hedging positions})

, computed from the weekly CFTC report (released each Friday but reporting positions from the previous Tuesday). The changes in the variables entering the regression are between consecutive Tuesdays.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 539 (weekly data from July 2006 to December 2016).]

		ETF flows	$\Delta$ term structure	$\Delta$ HP	$\Delta$ dollar	$\Delta r$	$R^{\textbf{2}}$
Crude oil	Estimate	0.07	$-$ 0.52	0.10	$-$ 0.10	0.13	0.33
	$p$ -value	0.05**	${<}\text{2}\text{e}{-}\text{16}$ ***	0.006***	0.005***	0.0002***
Gasoline	Estimate	0.07	$-$ 0.43	$-$ 0.28	$-$ 0.05	0.07	0.34
	$p$ -value	0.04**	${<}\text{2}\text{e}{-}\text{16}$ ***	$\text{1.4}\text{e}{-}\text{14}$ ***	0.16	0.05**
Heating oil	Estimate	0.06	$-$ 0.58	$-$ 0.21	$-$ 0.06	0.08	0.42
	$p$ -value	0.09*	${<}\text{2}\text{e}{-}\text{16}$ ***	0. $\text{2}\text{e}{-}\text{09}$ ***	0.08*	0.01**
Natural gas	Estimate	0.05	$-$ 0.50	$-$ 0.14	$-$ 0.05	0.16	0.24
	$p$ -value	0.17	${<}\text{2}\text{e}{-}\text{16}$ ***	0.0002***	0.19	$\text{3}\text{e}{-}\text{05}$ ***

Hedging pressure has a significant positive relation to the futures prices returns in the crude oil market, and a negative relation to the other three futures prices. The positive relation for crude oil is the one suggested by intuition due to the need to mitigate the demand for new long positions from hedgers. The negative relation in the three other cases could be the reflection of an endogeneity of commercial positions to the prices, as seen in Section 3.1.

Term structure enters in all cases with a negative sign, as expected, since term structure changes have a strong positive correlation to inventory variations (Table 2).

We observe a significant relation of index funds to futures prices for crude oil, gasoline and heating oil. A one-standard-deviation positive index flows is associated, for all four energy commodities, to an increase in prices by about 0.06 standard deviations.

4.4 Further tests and results discussion

Due to the price inelasticity of supply and demand in energy markets, it is possible that inventories react with a time lag of a few weeks to an abnormal price change in the paper market. For this purpose, we apply the same regression analysis, varying the time period between observation dates (Table 5).

Table 5: OLS regressions of the prices, term structure and inventory on index flows with different observation frequencies (NYMEX contracts). [Here we report the regression coefficients

\beta

(and their

p

-values in parentheses) of prices, term structure and inventory on ETF flows in the following regression models for crude oil, heating oil, gasoline and natural gas NYMEX contracts:

\text{futures returns}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\delta\Delta% \text{term structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{term structure}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\sum_{j% }\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{inventory}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\varepsilon_% {i,t}

. The observation frequencies vary from two observations per month (bimonthly) to three observations per year (every four months).

\text{ETF~{}flows}_{t}

denotes the net weekly inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in period

t

. Futures prices returns are computed for each commodity

I

by means of the returns of the strategy longing and rolling over the first-nearby futures contract at each last trading date.

\Delta\text{term~{}structure}_{i,t}

refers to the change in term structure for commodity

i

in period

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of the first-nearby contract.

\Delta\text{inventory}_{i,t}

is the weekly US inventory change, computed from the EIA report (released each Friday). We use the crude oil and refined petroleum products inventory in the crude oil regression. Natural gas inventories are calculated as deviations to the average inventory across the previous five years for the same week of the year. The control variables

x_{j,t}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

are defined in Table 3. The bimonthly models for prices and term structure (respectively, inventory) use observations made every other Tuesday (respectively, Friday). All the other models use observations made on the last Tuesday of the month.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. In most cases, we report only the regression coefficients whose

p

-value is less than 10%. Number of observations (from July 2006 to December 2016): 272 for bimonthly and 136 for monthly data; 66 for every two months, 44 for every three months and 28 for every four months.]

	Crude oil	Gasoline	Heating oil	Natural gas
Bimonthly
Prices	0.18 (0.0005***)	0.12 (0.02**)	0.14 (0.004***)	0.17 (0.03**)
Term structure				0.05 (0.42)
Inventories				0.07 (0.26)
Monthly
Prices	0.16 (0.02**)	0.18 (0.009***)	0.18 (0.01**)	0.17 (0.04**)
Term structure				0.16 (0.05**)
Inventories				0.23 (0.001***)
Every two months
Prices	0.23 (0.03**)	0.36 (0.002***)	0.32 (0.003***)	0.09 (0.46)
Term structure				$-$ 0.18(0.14)
Inventories				0.25 (0.03**)
Every three months
Prices	0.24 (0.13)	0.41 (0.04**)	0.33 (0.01**)	0.09 (0.55)
Term structure	$-$ 0.36 (0.03**)			0.17 (0.25)
Inventories				0.10 (0.56)
Every four months
Prices	0.13 (0.35)	0.55(0.001***)	0.03 (0.88)	0.12 (0.42)
Term structure	$-$ 0.43(0.01**)	$-$ 0.41(0.03**)		$-$ 0.04 (0.82)
Inventories				0.21 (0.27)

The relation of index flows to energy futures prices appears to be maximal over a period of one to two months for crude oil and natural gas, and three to four months for oil refined products. At the monthly horizon, a one-standard-deviation positive index flows is associated, for all four energy commodities, to an 0.17 standard deviations price rise. The regression coefficient reaches more than 0.3 for the two refined products when the period between the observation dates is between two and three months, and more than 0.5 for gasoline when observations are four months away. This observation suggests that there are nonlinear effects in the price response to index flows: prices respond to a series of aligned weekly index flows more strongly than predicted by the weekly regression model. This points to the existence of thresholds above which index speculation starts having a stronger impact on energy prices. The flows/price relation vanishes for all energy commodities bar gasoline when observations are made every four months. Hence, our results suggest that it takes about one quarter for energy prices to revert after being pushed away from their fundamental value by uninformed speculative flows in the short term.

We have also varied the period of analysis to further test the robustness of the results (Table 6). The correlation of index flows to energy prices reached its apogee during the 2008 financial crisis and receded after the peak of commodities prices observed in 2011.

Table 6: Subsample regressions (NYMEX contracts). [Here we report the regression coefficients

\beta

(and their

p

-values in parentheses) of prices, term structure and inventory on ETF flows in the following weekly regression models for crude oil, heating oil, gasoline and natural gas NYMEX contracts:

\text{futures returns}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\delta\Delta% \text{term structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{term structure}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\sum_{j% }\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{inventory}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\varepsilon_% {i,t}

. The regressions are run over different subperiods. (1) June 2006–June 30, 2008 (boom). Number of weekly observations: 98. (2) July 2008–January 31, 2009 (collapse). Number of weekly observations: 29. (3) February 2009–March 31, 2011 (recovery). Number of weekly observations: 113. (4) April 2011–2016 (recent fall). Number of weekly observations: 298.

\text{ETF~{}flows}_{t}

denotes the net weekly inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

. Futures prices returns are computed for each commodity

i

by means of the returns of the strategy longing and rolling over the first-nearby futures contract at each last trading date.

\Delta\text{term~{}structure}_{i,t}

refers to the change in term structure of commodity

i

in period

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of the first-nearby contract.

\Delta\text{inventory}_{i,t}

is the weekly US inventory change in the United States, computed from the EIA report (released each Friday). We use the crude oil and refined petroleum products inventory in the crude oil regression. Natural gas inventories are calculated as deviations of the average inventory across the previous five years for the same week of the year. The control variables

x_{j,t}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

are defined in Table 3. The regressions of prices and term structure (respectively, inventory) use observations made every Tuesday (respectively, Friday).

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. We report only the regression coefficients whose

p

-value is less than 10%.]

		Prices	Term structure	Inventories
Boom	Crude oil	0.28 (0.001***)
	Gasoline	0.13 (0.07*)
	Heating oil	0.17 (0.03**)	$-$ 0.21 (0.04**)
	Natural gas
Collapse	Crude oil
	Gasoline	0.41 (0.02**)
	Heating oil	0.45 (0.003***)
	Natural gas	0.17 (0.09*)
Recovery	Crude oil	0.19 (0.02**)
	Gasoline	0.16 (0.03**)
	Heating oil	0.17 (0.02**)	$-$ 0.23 (0.01**)
	Natural gas	0.10 (0.05**)
Recent fall	Crude oil	0.10 (0.04**)
	Gasoline
	Heating oil			$-$ 0.11(0.06*)
	Natural gas

From the previous analysis, we draw three main conclusions. First, index flows have a positive relation to crude oil, gasoline and heating oil futures prices at the weekly level and with all four energy prices at the monthly level. It is important to recall here that we are faced with a severe endogeneity problem, since the commodity indexes that serve as underlyings to the three ETFs considered have a very strong positive correlation to the oil prices. Hence, we expect some of the flows to these ETFs to be “trend following” in nature, ie, to be driven by the oil price itself. Therefore, the obtained regression coefficients are probably an upper bound of the actual “impact” of index flows on the prices.

Second, there are strong linear effects in the index flows/prices reaction. Our results suggest that the response of energy prices to index flows is maximal over a period of one to two months.

Third, we find evidence of an impact of index funds on inventory or the term structure only in the natural gas market (within a monthly observation frequency).

On several occasions, we find a negative relation of index flows to the term structure without any similar effect on real inventory data (this is observed for heating oil in the two boom periods and gasoline/crude oil when observations are four months apart). This could be the reflection of a buying pressure exerted by index investors on short-dated contracts (index investors roll over the first-nearby contract) relative to long-dated contracts.

The bulk of our observations therefore lend support to the hypothesis of Pierru and Babusiaux (2010): uninformed speculative activity might influence commodities futures prices, but, since this effect is short-lived and supply and demand are inelastic in the short-term, this impact does not involve stockpiling as a signature. These results are in line with previous empirical literature on the oil market (see, for example, Lombardi and Robays 2011; Hamilton 2009).

The case of the natural gas market deserves some specific comments. Our results show that, over a monthly horizon, prices, index flows and inventories tend to align with one another. The relation of index flows to natural gas prices is only present at the monthly time horizon. However, the positive relation of index flows to inventories persists over a period of several months, although it is statistically significant only over a period of one to two months. Further, unreported regressions introducing crude oil returns as a control variable show that the relation of index flows to natural gas prices is driven by the oil market. All in all, these different results suggest that natural gas prices respond to index flows through the mediation of crude oil prices. This could possibly explain the absence of relation at horizons shorter than a month, since lag time is required for natural gas to respond to an oil price shock induced by index investors (see Hartley et al 2008). The positive relation of index flows to prices dissipates over longer time frames, pointing to faster price correction mechanisms in the natural gas market compared with the oil market. The effect of index flows on inventories suggests a relatively important price elasticity in the supply of natural gas to the United States in the medium term. The US natural gas market is indeed mostly local, in contrast with the three oil-related markets, and regional production is highly responsive to market price fluctuations.

5 Extension to agricultural commodities

In this section, we apply our framework of analysis to twelve US-based agricultural markets. The motivation behind this extension is that index flows are more exogenous to these markets, whose correlation to global commodity indexes is weaker than that of energy markets. Another characteristic of agricultural products is the relative price inelasticity of the supply, due in particular to the rigid planting and harvesting cycles.

Tables 7 and 8 show the results of three index flows–inventory and flows–futures returns regressions on weekly data.

Table 7: Regression of prices and term structure changes on index flows for twelve US-traded agricultural contracts. [Here we report the regression coefficients

\beta

(and their

p

-values in parentheses) of prices and term structure on ETF flows in the following regression models for twelve US-traded agricultural contracts:

\text{futures returns}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\delta\Delta% \text{term structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{term structure}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\sum_{j% }\gamma_{j}x_{j,t}+\varepsilon_{i,t}

.

\text{ETF~{}flows}_{t}

denotes the net weekly inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

. Futures prices returns are computed by means of the returns of the strategy longing and rolling over the first-nearby futures contract at the last trading date.

\Delta\text{term structure}_{i,t}

refers to the change in term structure of commodity

i

in week

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of each contract. The control variables are

x_{j,t}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

.

\Delta r

is the change in the six-month government bill rate.

\Delta\text{dollar}

represents the dollar index return.

\Delta\text{HP}

refers to the change in hedging pressure, which is calculated from the weekly variation of the ratio

(\text{long hedging positions}-\text{short hedging positions})/(\text{long % hedging positions}+\text{short hedging positions})

, computed from the weekly CFTC report (released each Friday but reporting positions from the previous Tuesday). The changes in the variables entering the regression are between consecutive Tuesdays.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 538 (weekly data from July 2006 to December 2016).]

	Prices	Term structure
Cocoa NYBOT	0.06 (0.08*)
Coffee NYBOT	0.06 (0.08*)
Cotton NYBOT	0.10 (0.003***)
Sugar NYBOT
Feeder cattle CME
Lean hogs CME
Live cattle CME
Corn CBOT	0.12 (0.001***)
Soybeans CBOT	0.10 (0.001***)
Soybean oil CBOT	0.14 (0.0001***)	$-$ 0.06 (0.10*)
Wheat CBOT	0.09 (0.02**)
Wheat KCBOT	0.12 (0.001***)

Table 8: OLS regressions of prices and term structure on index flows with different observation frequencies (twelve US-traded agricultural contracts). [Here we report the regression coefficients

\beta

(and their

p

-values in parentheses) of prices and term structure on ETF flows in the following regression models for twelve US-traded agricultural contracts:

\text{futures returns}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\delta\Delta% \text{term structure}_{i,t}+\sum_{j}\gamma_{j}x_{j,t}+\varepsilon_{i,t}

,

\Delta\text{term structure}_{i,t}=\alpha+\beta\,\text{ETF~{}flows}_{t}+\sum_{j}\gamma_{j}x_{j,t% }+\varepsilon_{i,t}

.

\text{ETF~{}flows}_{t}

denotes the net inflows into the three ETF tracking generalist commodity indexes, the GSCI, the Bloomberg Commodity Index and the Deutsche Bank Commodity Index, in week

t

. Futures prices returns are computed by means of the returns of the strategy longing and rolling over the first-nearby futures contract at the last trading date.

\Delta\text{term structure}_{i,t}

refers to the change in term structure of commodity

i

in week

t

. The term structure is obtained from the cumulative return of a strategy shorting the first-nearby futures contracts, longing the futures contract delivering one year after the first-nearby contract, and rolling over this spreading position at the last trading date of each contract. The control variables are

{x_{j,t}}=(\Delta r,\Delta\text{dollar},\Delta\text{HP})

.

\Delta r

is the change in the six-month government bill rate.

\Delta\text{dollar}

represents the dollar index return.

\Delta\text{HP}

refers to the change in hedging pressure, which is calculated from the weekly variation of the ratio

(\text{long hedging positions}-\text{short hedging positions})/(\text{long % hedging positions}+\text{short hedging positions})

, computed from the weekly CFTC report (released each Friday but reporting positions from the previous Tuesday). The bimonthly models use observations made every other Tuesday. The two other models use observations made on the last Tuesday of the month.

p

-values are reported in parentheses.

{}^{***}

Significant at 1%.

{}^{**}

Significant at 5%.

{}^{*}

Significant at 10%. All variables are standardized. Number of observations: 287 for bimonthly and 132 for monthly data, and 63 for every two months (from July 2006 to December 2016).]

	Bimonthly		Monthly		Every two months

	Prices	Term structure	Prices	Term structure	Prices	Term structure
Cocoa	0.16 (0.002***)
Coffee		$-$ 0.10 (0.05**)
Cotton
Sugar	0.08 (0.06*)
Feeder cattle
Lean hogs
Live cattle
Corn	0.13 (0.007***)		0.13 (0.06*)
Soybeans	0.15 (0.001***)
Soybean oil	0.17 (0.001***)		0.16 (0.02*)
Wheat CBOT	0.10 (0.04**)		0.17 (0.02**)
Wheat KCBOT	0.14 (0.003***)		0.17 (0.02**)

Again, we find strong evidence of a positive impact of index flows on commodities’ prices for all agricultural markets bar animal products (in line with Guilleminot et al (2014)). Similarly to energy commodities, the coefficient of the relation gains in strength when the period between observation dates is two weeks. However, the effect vanishes for soft commodities over time horizons longer than two weeks, and for grains when observation dates are distant by more than one month. Hence, the abnormal impact of index flows is more rapidly corrected in the soft commodities’ markets than in the grains markets. In addition, the pace of correction is faster for agricultural markets as a whole than for energy markets, which suggests that agricultural markets are more tied to supply-and-demand fundamentals than energy markets. Again, we are faced with an “oil endogenity problem”, which could be expressed as follows. Since index investors follow the oil price trends and agricultural prices are correlated to energy markets – in particular, through demand from the biofuel industry – the relation of agricultural prices to index flows could be due to index flows and agricultural prices being jointly driven by oil price fluctuations. To alleviate this concern, we have run unreported regressions showing that the index flows–price relation is robust to the introduction of oil price returns as a control variable. This has two implications. First, it allows us to reject the idea that the “oil endogeneity” hypothesis can entirely explain the observed relation of ETF flows to agricultural prices. Second, it reveals that index flows have an impact not only on the absolute agricultural price levels but also on the relative pricing of agricultural commodities to oil. This “relative pricing” impact may be due to the lower liquidity of agricultural markets relative to the oil market, resulting in an increased difficulty in absorbing exogenous index flows in the agricultural markets.

However, we find no evidence supporting a positive impact of index flows on the term structure of agricultural futures prices.⁴⁴Unreported regressions on the grain markets show that the term structure variations again have a strong positive correlation to changes in the stock-to-use ratios, derived from the monthly United States Department of Agriculture (World Agricultural Supply and Demand Estimates) reports, and that index flows do not correlate to the changes in the stock-to-use ratios at the monthly level. Similarly to energy markets, we uncover traces of a negative relation of index flows to the term structure (soybean oil at the weekly horizon and coffee at the bimonthly horizon).

Overall, our results again suggest that index funds flows have a significant short-term impact on some agricultural commodities’ futures prices, but that this impact does not go through stockpiling. These findings are broadly consistent with our previous results on energy commodities, the main difference being that with energy commodities the faster pace at which index speculators’ abnormal impacts on prices are corrected.

6 Conclusion

The impact of index speculation on commodity prices has garnered much attention in discussions concerning the financialization of commodity markets.

Motivated by the debate on how the impact of index funds activities on commodities’ prices is channeled, this paper investigates the influence of index flows on commodities’ prices, inventories and futures prices term structure. By using flows on the three main generalist commodity ETFs as an independent variable, we have studied the relation of index flows to the prices, term structure and inventories of four energy commodities, before extending the analysis to twelve US-traded agricultural contracts.

Our results can be summarized as follows. First, index flows are found to have no significant positive relation to either the EIA weekly inventory measures or the futures prices term structure. However, a significant positive relation of index flows to futures prices is found for a large proportion of energy and agricultural commodities. These empirical results support the theoretical hypothesis of Pierru and Babusiaux (2010) that index funds flows may have a direct impact on the futures prices that does not necessarily involve stockpiling as a signature.

Second, according to some additional tests, the relation of index flows to futures prices appears to be strongly nonlinear: the estimated “impact” of index flows increases when measured over horizons of longer than the week. However, the impact recedes for agricultural (respectively, energy) products when the horizon is longer than two weeks (respectively, two months). These results suggest that index flows have more of an impact after they breach certain thresholds, but that, beyond certain levels of speculation, some correction mechanisms intervene to make prices revert to their fundamental level.

As a conclusion, index speculation can impact commodity futures prices without stockpiling as a signature. There are two implications of this result. First, it sheds light on the price formation mechanisms in spot and paper commodity markets. We now have strong evidence that the demand from unspecialized financial investors in the paper market significantly distorts price formation mechanisms. Also, the absence of a link between index flows and inventories or the term structure confirms the price inelasticity of supply and demand in the short run, resulting in the existence of a large range of possible short-run price equilibriums. Index speculation is susceptible to temporarily shift the market equilibrium without triggering any real effects on supply or demand. Second, from a regulatory perspective, the evidence that commodity index funds affect futures prices up to a horizon of several weeks or several months but not over longer time scales suggests a certain short-term inefficiency of commodities markets, as informed traders seem to take a certain amount of time to correct the artificial price moves induced by uninformed speculators.

Declaration of interest

The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.

References

Borovkova, S. (2003). Detecting market transitions: from backwardation to contango and back. Energy Power Risk Management 8(3), 46–49.
Büyüksahin, B., and Harris, J. H. (2011). Do speculators drive crude oil futures prices? Energy Journal 32(2), 167–202 (https://doi.org/10.5547/ISSN0195-6574-EJ-Vol32-No2-7).
Capelle-Blancard, G., and Coulibaly, D. (2011). Index trading and agricultural commodity prices: a panel Granger causality analysis. International Economics 126/127, 51–72 (https://doi.org/10.1016/S2110-7017(13)60036-0).
Fama, E. F., and French, K. R. (1988). Business cycles and the behavior of metals prices. Journal of Finance 43(5), 1075–1093 (https://doi.org/10.1111/j.1540-6261.1988.tb03957.x).
Geman, H., and Ohana, S. (2009). Forward curves, scarcity and price volatility in oil and natural gas markets Energy Economics 31(4), 576–585 (https://doi.org/10.1016/j.eneco.2009.01.014).
Gilbert, C., and Pfuderer, S. (2014). The role of index trading in price formation in the grains and oilseeds markets. Journal of Agricultural Economics 65(2), 303–322 (https://doi.org/10.1111/1477-9552.12068).
Gorton, G., Hayashi, F., and Rouwenhorst, K. (2007). The fundamentals of commodity futures returns. Working Paper 07-08 2007, Yale ICF.
Grosche, S. (2014). What does Granger causality prove? A critical examination of the interpretation of Granger causality results on price effects of index trading in agricultural commodity markets. Journal of Agricultural Economics 65(2), 279–302 (https://doi.org/10.1111/1477-9552.12058).
Guilleminot, B., Ohana, J. J., and Ohana, S. (2014). The interaction of speculators and index investors in agricultural derivatives markets. Agricultural Economics 45(6), 767–792 (https://doi.org/10.1111/agec.12122).
Hamilton, J. D. (2009). Causes and consequences of the oil shock of 2007–08. Working Paper 15002, National Bureau of Economic Research.
Hartley, P. R., Medlock, K. B., III, and Rosthal, J. E. (2008). The relationship of natural gas to oil prices. Energy Journal 29(3), 47–65 (https://doi.org/10.5547/ISSN0195-6574-EJ-Vol29-No3-3).
Henderson, B. J., Pearson, N. D., and Wang, L. (2014). New evidence on the financialization of commodity markets. Review of Financial Studies 28(5), 1285–1311 (https://doi.org/10.1093/rfs/hhu091).
Irwin, S. H., and Sanders, D. R. (2010). The impact of index and swap funds in commodity futures markets. Report, Organisation for Economic Co-operation and Development (OECD) (https://doi.org/10.1787/5kmd40wl1t5f-en).
Irwin, S. H., and Sanders, D. R. (2011). Index funds, financialization, and commodity futures markets. Applied Economic Perspectives and Policy 33, 1–31 (https://doi.org/10.1093/aepp/ppq032).
Keynes, J. M. (1930). A treatise on money. In The Applied Theory of Money, Volume 2. Harcourt, Brace & Co.
Krugman, P. (2008a). The oil nonbubble. New York Times, May 12.
Krugman, P. (2008b). Sepculative nonsense, once again. New York Times, June 23.
Lombardi, M. J., and Robays, V. (2011). Do financial investors destabilize the oil prices? Working Paper 1346, European Central Bank.
Masters, M. W. (2008). Testimony before the Committee on Homeland Security and Government Affairs US Senate. US Senate, Washington, DC.
Moskowitz, T., Ooi, Y., and Pedersen, L. (2012). Time series momentum. Journal of Financial Economics 104, 228–250 (https://doi.org/10.1016/j.jfineco.2011.11.003).
Mou, Y. (2011). Limits to arbitrage and commodity index investment: front-running the Goldman Roll. Working Paper, Social Science Research Network.
Pierru, A., and Babusiaux, D. (2010). Speculation without oil stockpiling as a signature: a dynamic perspective. Working Paper 10-004, Center for Energy and Environmental Policy Research.
Pirrong, C. (2008). Stochastic fundamental volatility, speculation, and commodity storage. Working Paper, Social Science Research Network (https://doi.org/10.2139/ssrn.1340658).
Robles, M., Torero, M., and von Braun, J. (2009). When speculation matters. Issue Brief, International Food Policy Research Institute, Washington, DC.
Sanders, D. R., and Irwin, S. H. (2017). Bubbles, froth, and facts: another look at the Masters hypothesis in commodity futures markets. Journal of Agricultural Economics 68(2), 345–365 (https://doi.org/10.1111/1477-9552.12191).
Singleton, K. J. (2013). Investor flows and the 2008 boom/bust in oil prices. Management Science 60(2), 300–318 (https://doi.org/10.1287/mnsc.2013.1756).
Telser, L. G. (1958). Futures trading and the storage of cotton and wheat. Journal of Political Economy 66(3), 233–255 (https://doi.org/10.1086/258036).
Working, H. (1933). Price relations between July and September wheat futures at Chicago since 1885. Wheat Studies 06.
Working, H. (1949). The theory of the price of storage. American Economic Review 39, 1254–1262.

[bib.bib2] Borovkova, S. (2003). Detecting market transitions: from backwardation to contango and back. Energy Power Risk Management 8(3), 46–49.

[bib.bib4] Büyüksahin, B., and Harris, J. H. (2011). Do speculators drive crude oil futures prices? Energy Journal 32(2), 167–202 (https://doi.org/10.5547/ISSN0195-6574-EJ-Vol32-No2-7).

[bib.bib6] Capelle-Blancard, G., and Coulibaly, D. (2011). Index trading and agricultural commodity prices: a panel Granger causality analysis. International Economics 126/127, 51–72 (https://doi.org/10.1016/S2110-7017(13)60036-0).

[bib.bib8] Fama, E. F., and French, K. R. (1988). Business cycles and the behavior of metals prices. Journal of Finance 43(5), 1075–1093 (https://doi.org/10.1111/j.1540-6261.1988.tb03957.x).

[bib.bib10] Geman, H., and Ohana, S. (2009). Forward curves, scarcity and price volatility in oil and natural gas markets Energy Economics 31(4), 576–585 (https://doi.org/10.1016/j.eneco.2009.01.014).

[bib.bib12] Gilbert, C., and Pfuderer, S. (2014). The role of index trading in price formation in the grains and oilseeds markets. Journal of Agricultural Economics 65(2), 303–322 (https://doi.org/10.1111/1477-9552.12068).

[bib.bib14] Gorton, G., Hayashi, F., and Rouwenhorst, K. (2007). The fundamentals of commodity futures returns. Working Paper 07-08 2007, Yale ICF.

[bib.bib16] Grosche, S. (2014). What does Granger causality prove? A critical examination of the interpretation of Granger causality results on price effects of index trading in agricultural commodity markets. Journal of Agricultural Economics 65(2), 279–302 (https://doi.org/10.1111/1477-9552.12058).

[bib.bib18] Guilleminot, B., Ohana, J. J., and Ohana, S. (2014). The interaction of speculators and index investors in agricultural derivatives markets. Agricultural Economics 45(6), 767–792 (https://doi.org/10.1111/agec.12122).

[bib.bib20] Hamilton, J. D. (2009). Causes and consequences of the oil shock of 2007–08. Working Paper 15002, National Bureau of Economic Research.

[bib.bib22] Hartley, P. R., Medlock, K. B., III, and Rosthal, J. E. (2008). The relationship of natural gas to oil prices. Energy Journal 29(3), 47–65 (https://doi.org/10.5547/ISSN0195-6574-EJ-Vol29-No3-3).

[bib.bib24] Henderson, B. J., Pearson, N. D., and Wang, L. (2014). New evidence on the financialization of commodity markets. Review of Financial Studies 28(5), 1285–1311 (https://doi.org/10.1093/rfs/hhu091).

[bib.bib26] Irwin, S. H., and Sanders, D. R. (2010). The impact of index and swap funds in commodity futures markets. Report, Organisation for Economic Co-operation and Development (OECD) (https://doi.org/10.1787/5kmd40wl1t5f-en).

[bib.bib28] Irwin, S. H., and Sanders, D. R. (2011). Index funds, financialization, and commodity futures markets. Applied Economic Perspectives and Policy 33, 1–31 (https://doi.org/10.1093/aepp/ppq032).

[bib.bib30] Keynes, J. M. (1930). A treatise on money. In The Applied Theory of Money, Volume 2. Harcourt, Brace & Co.

[bib.bib32] Krugman, P. (2008a). The oil nonbubble. New York Times, May 12.

[bib.bib34] Krugman, P. (2008b). Sepculative nonsense, once again. New York Times, June 23.

[bib.bib36] Lombardi, M. J., and Robays, V. (2011). Do financial investors destabilize the oil prices? Working Paper 1346, European Central Bank.

[bib.bib38] Masters, M. W. (2008). Testimony before the Committee on Homeland Security and Government Affairs US Senate. US Senate, Washington, DC.

[bib.bib40] Moskowitz, T., Ooi, Y., and Pedersen, L. (2012). Time series momentum. Journal of Financial Economics 104, 228–250 (https://doi.org/10.1016/j.jfineco.2011.11.003).

[bib.bib42] Mou, Y. (2011). Limits to arbitrage and commodity index investment: front-running the Goldman Roll. Working Paper, Social Science Research Network.

[bib.bib44] Pierru, A., and Babusiaux, D. (2010). Speculation without oil stockpiling as a signature: a dynamic perspective. Working Paper 10-004, Center for Energy and Environmental Policy Research.

[bib.bib46] Pirrong, C. (2008). Stochastic fundamental volatility, speculation, and commodity storage. Working Paper, Social Science Research Network (https://doi.org/10.2139/ssrn.1340658).

[bib.bib48] Robles, M., Torero, M., and von Braun, J. (2009). When speculation matters. Issue Brief, International Food Policy Research Institute, Washington, DC.

[bib.bib50] Sanders, D. R., and Irwin, S. H. (2017). Bubbles, froth, and facts: another look at the Masters hypothesis in commodity futures markets. Journal of Agricultural Economics 68(2), 345–365 (https://doi.org/10.1111/1477-9552.12191).

[bib.bib52] Singleton, K. J. (2013). Investor flows and the 2008 boom/bust in oil prices. Management Science 60(2), 300–318 (https://doi.org/10.1287/mnsc.2013.1756).

[bib.bib54] Telser, L. G. (1958). Futures trading and the storage of cotton and wheat. Journal of Political Economy 66(3), 233–255 (https://doi.org/10.1086/258036).

[bib.bib56] Working, H. (1933). Price relations between July and September wheat futures at Chicago since 1885. Wheat Studies 06.

[bib.bib58] Working, H. (1949). The theory of the price of storage. American Economic Review 39, 1254–1262.

Journal of Energy Markets

Does the impact of exchange-traded funds flows on commodities prices involve stockpiling as a signature? An empirical investigation

Steve Ohana and Xiaoying Huang

Follow

Need to know

Abstract

Introduction

1 Introduction

2 Theoretical background

3 Term structure and index funds

3.1 Term structure and its determinants

3.1.1 Interest rates

3.1.2 Dollar index

3.1.3 Hedging pressure

3.2 Commodity ETF flows

4 Empirical analysis

4.1 Primary analysis using weekly EIA inventory data

4.2 Term structure and index funds flows

4.3 Index funds and futures prices

4.4 Further tests and results discussion

5 Extension to agricultural commodities

6 Conclusion

Declaration of interest

References

All issues

Browse journals

You are currently on corporate access.